Whittaker–Shannon interpolation formula
The Whittaker–Shannon interpolation formula or sinc interpolation is a method to reconstruct a continuous-time bandlimited signal from a set of equally spaced samples.
Contents |
Definition
The interpolation formula, as it is commonly called, dates back to the works of E. Borel in 1898, and E. T. Whittaker in 1915, and was cited from works of J. M. Whittaker in 1935, and in the formulation of the Nyquist–Shannon sampling theorem by Claude Shannon in 1949. It is also commonly called Shannon's interpolation formula and Whittaker's interpolation formula. E. T. Whittaker, who published it in 1915, called it the Cardinal series.
The sampling theorem states that, under certain limiting conditions, a function x(t) can be recovered exactly from its samples, x[n] = x(nT), by the Whittaker–Shannon interpolation formula:
where T = 1/fs is the sampling interval, fs is the sampling rate, and sinc(x) is the normalized sinc function.
Validity condition
If the function x(t) is bandlimited, and sampled at a high enough rate, the interpolation formula is guaranteed to reconstruct it exactly. Formally, if there exists some B ≥ 0 such that
- the function x(t) is bandlimited to bandwidth B; that is, it has a Fourier transform
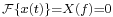 for |f| > B; and
for |f| > B; and - the sampling rate, fs, exceeds the Nyquist rate, twice the bandwidth: fs > 2B. Equivalently:
then the interpolation formula will exactly reconstruct the original x(t) from its samples. Otherwise, aliasing may occur; that is, frequencies at or above fs/2 may be erroneously reconstructed. See Aliasing for further discussion on this point.
Interpolation as convolution sum
The interpolation formula is derived in the Nyquist–Shannon sampling theorem article, which points out that it can also be expressed as the convolution of an infinite impulse train with a sinc function:
This is equivalent to filtering the impulse train with an ideal (brick-wall) low-pass filter.
Convergence
The interpolation formula always converges absolutely and locally uniform as long as
By the Hölder inequality this is satisfied if the sequence ![\scriptstyle (x[n])_{n\in\Z}](/2012-wikipedia_en_all_nopic_01_2012/I/75410a026c34daba17a2b32d2b5bbecc.png) belongs to any of the
belongs to any of the 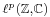 spaces with 1 < p < ∞, that is
spaces with 1 < p < ∞, that is
This condition is sufficient, but not necessary. For example, the sum will generally converge if the sample sequence comes from sampling almost any stationary process, in which case the sample sequence is not square summable, and is not in any 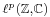 space.
space.
Stationary random processes
If x[n] is an infinite sequence of samples of a sample function of a wide-sense stationary process, then it is not a member of any 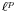 or Lp space, with probability 1; that is, the infinite sum of samples raised to a power p does not have a finite expected value. Nevertheless, the interpolation formula converges with probability 1. Convergence can readily be shown by computing the variances of truncated terms of the summation, and showing that the variance can be made arbitrarily small by choosing a sufficient number of terms. If the process mean is nonzero, then pairs of terms need to be considered to also show that the expected value of the truncated terms converges to zero.
or Lp space, with probability 1; that is, the infinite sum of samples raised to a power p does not have a finite expected value. Nevertheless, the interpolation formula converges with probability 1. Convergence can readily be shown by computing the variances of truncated terms of the summation, and showing that the variance can be made arbitrarily small by choosing a sufficient number of terms. If the process mean is nonzero, then pairs of terms need to be considered to also show that the expected value of the truncated terms converges to zero.
Since a random process does not have a Fourier transform, the condition under which the sum converges to the original function must also be different. A stationary random process does have an autocorrelation function and hence a spectral density according to the Wiener–Khinchin theorem. A suitable condition for convergence to a sample function from the process is that the spectral density of the process be zero at all frequencies equal to and above half the sample rate.
![x(t) = \sum_{n=-\infty}^{\infty} x[n] \cdot {\rm sinc}\left(\frac{t - nT}{T}\right)\,](/2012-wikipedia_en_all_nopic_01_2012/I/946207f70f194bb9c56133577ffc0144.png)
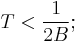
![x(t) = \left( \sum_{n=-\infty}^{\infty} x[n]\cdot \delta \left( t - nT \right) \right) *
{\rm sinc}\left(\frac{t}{T}\right).](/2012-wikipedia_en_all_nopic_01_2012/I/3937f3a9594cae525350ef02090f275b.png)
![\sum_{n\in\Z,\,n\ne 0}\left|\frac{x[n]}n\right|<\infty.](/2012-wikipedia_en_all_nopic_01_2012/I/dddf39c1f4ff3924322a4254eefdb237.png)
![\sum_{n\in\Z}\left|x[n]\right|^p<\infty.](/2012-wikipedia_en_all_nopic_01_2012/I/04b6d74a1819d7c7506a2f30c2ecd0a4.png)